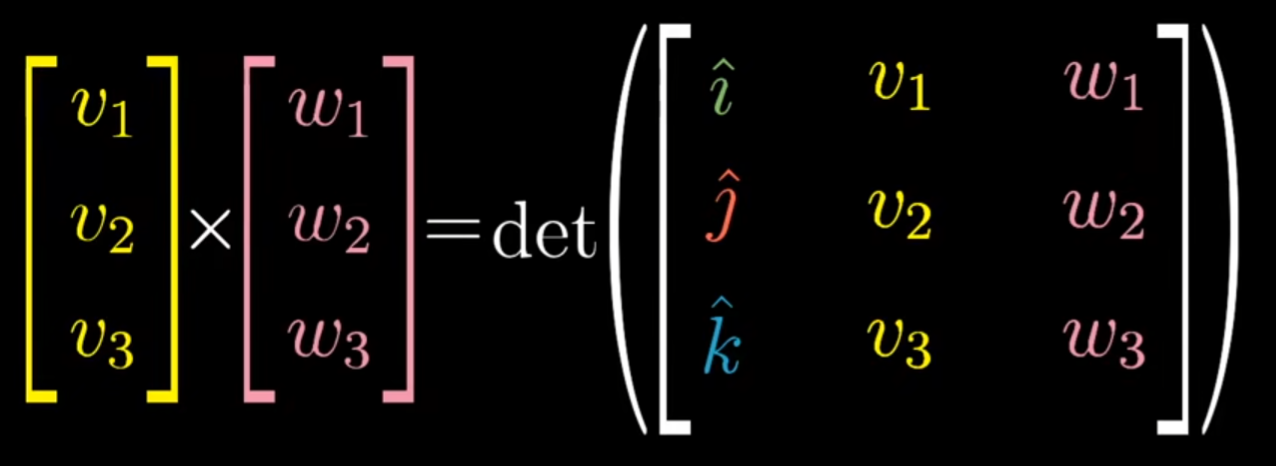叉积
叉积的结果不是一个数,而是一个向量。这个向量的长度就是两个向量所组成四边形的面积。
大致的说向量v和w组成的平行四边形的面积就是它们的叉积。

顺序会对叉积的结果有影响
$$
\vec v \times \vec w
$$
如果向量v在向量w的左侧,那么它们的叉积为负,也就是负的面积。如果向量v在向量w右侧,那么它们的叉积为正,也就是正的面积。
$$
\vec v \times \vec w = - \vec w \times \vec v
$$
对于顺序对结果的影响可以这样记
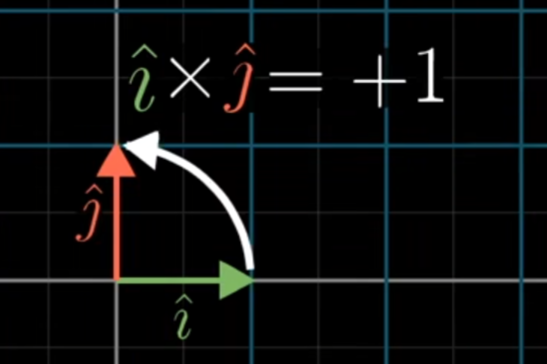
一个普通的二维平面i-hat和j-hat组成的面积,或者说点积就是正的。而i-hat在j-hat右侧。

因为基向量所组成的四边形面积为1,它又是从一个基向量变换过来的,所以向量v与向量w的叉积就是行列式的值。由于变换后向量v在向量w的左边,所以值为负。
所以这里向量v与向量w的叉积就是3*-1 - 2*1 = -5。
叉积的极大值
当向量v与向量w互相垂直的时候,叉积的绝对值出现最大值,因为垂直组成的四边形面积最大。
叉积的值
$$
\vec v \times \vec w = \vec p
$$
向量p的长度就是向量v与向量w所组成的四边形的面积
向量p垂直与 向量v和向量w
但是垂直与向量v和向量w的向量有两个,我们可以通过以下方式得出是哪个向量。
右手定则
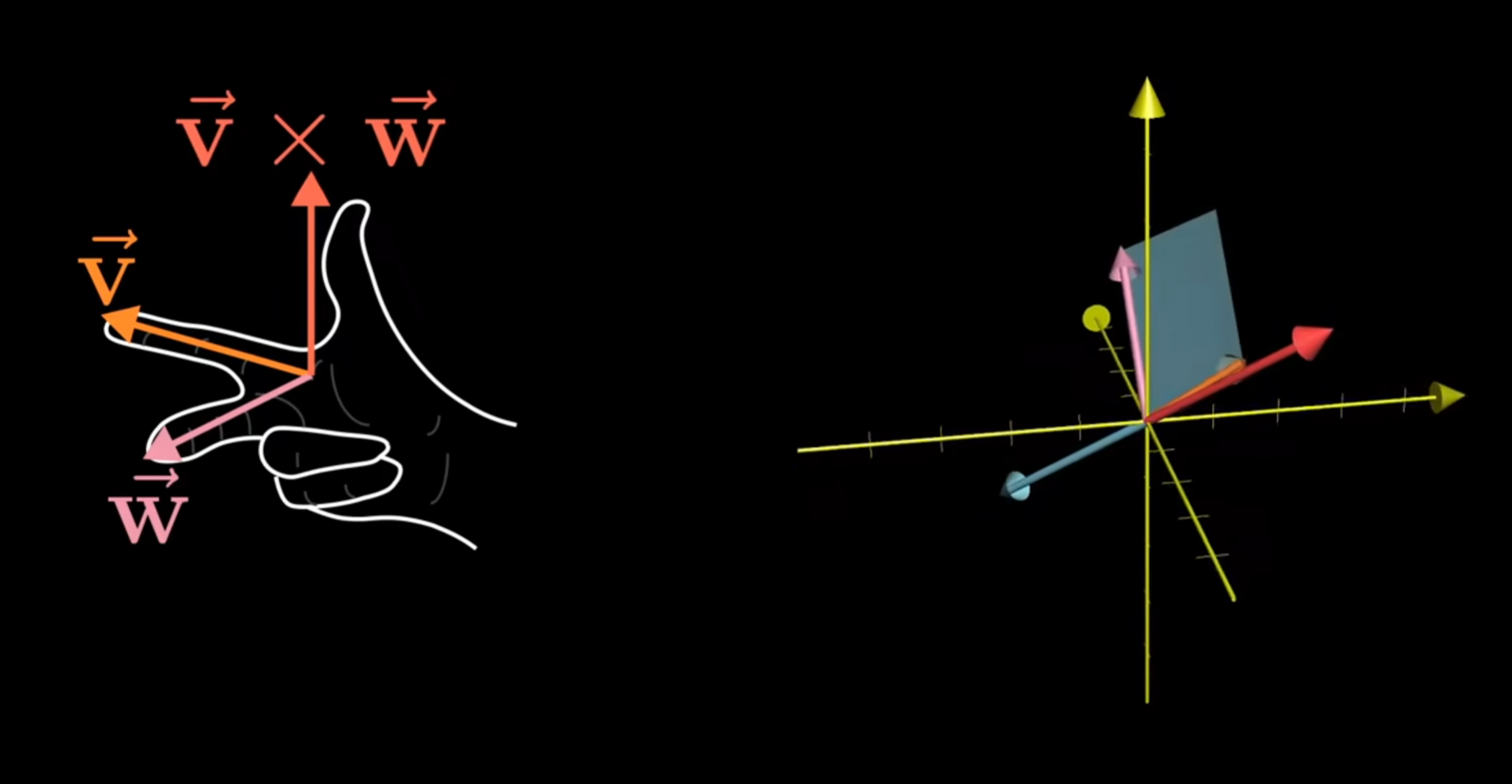
公式
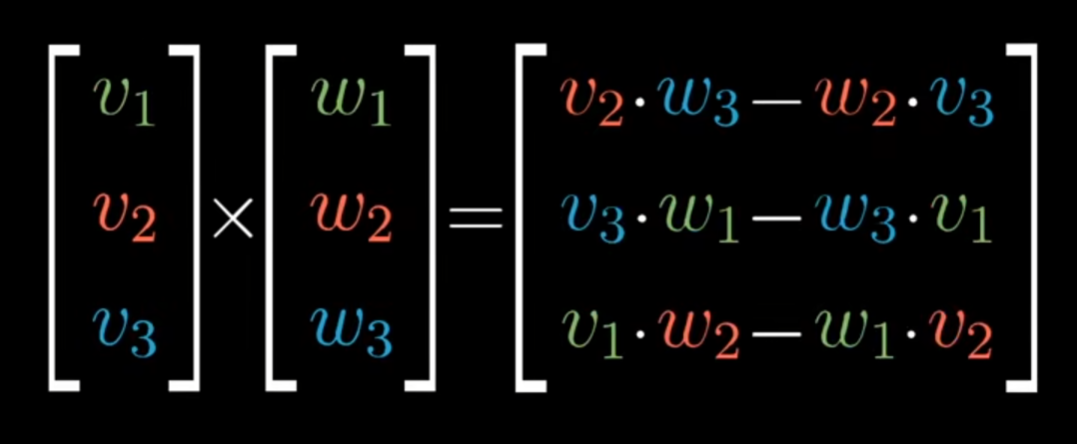
实际上也是计算行列式