点积
点积如何计算
$$
\begin{bmatrix}
1\\
2
\end{bmatrix}
\cdot
\begin{bmatrix}
3\\
4
\end{bmatrix}
=
1\cdot3 + 2\cdot4
$$
同理的多维向量之间的点积也是如此计算的。
几何上的点积

如果向量w与向量v方向相反,则应该加上负号。
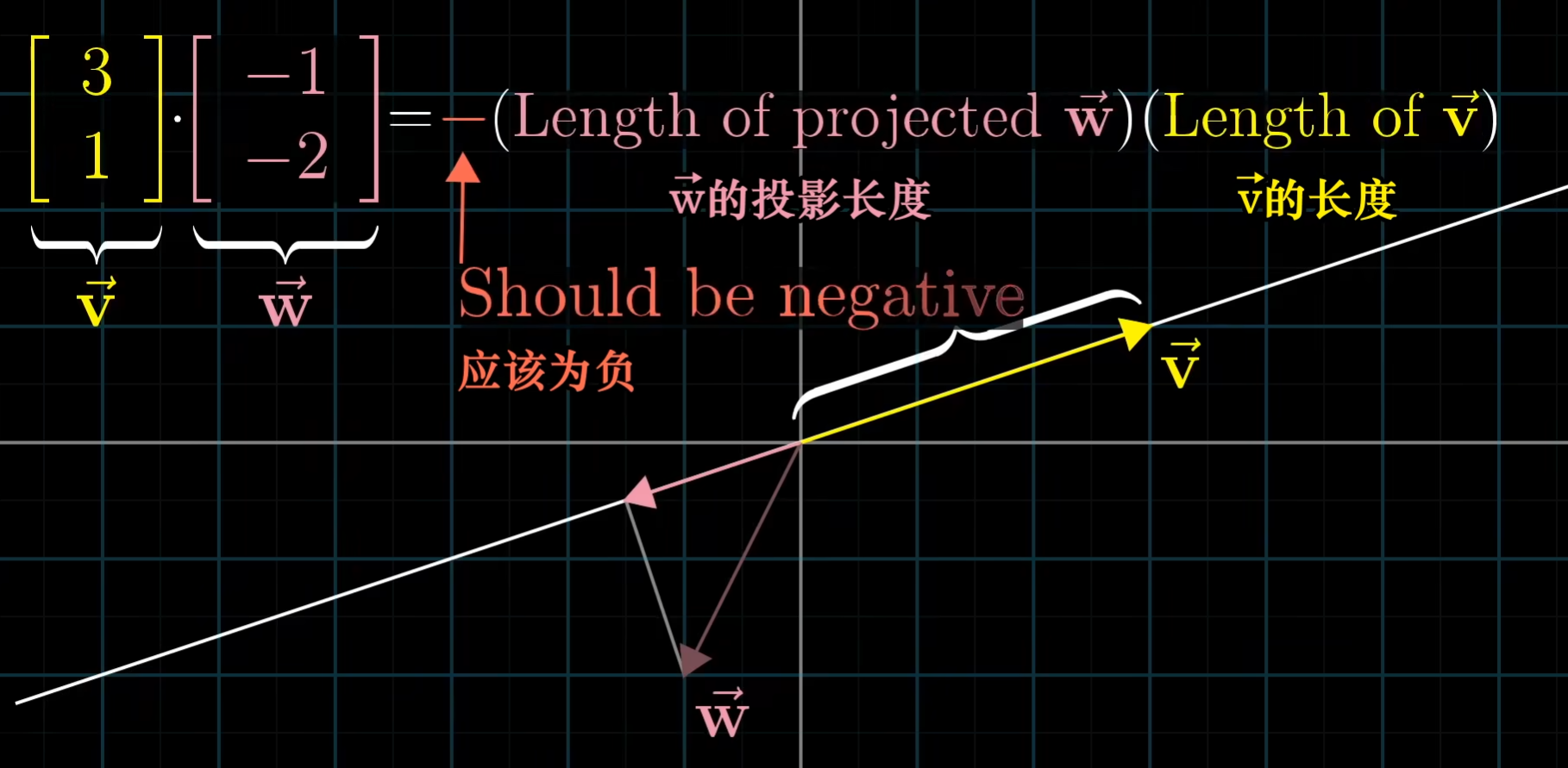
点积的意义
- 如果一个向量与另外一个向量的点积是正值,那么它们的方向大致相同。
- 如果一个向量与另外一个向量的点积为零,那么它们相互垂直。
- 如果一个向量与另外一个向量的点积为负值,那么它们的方向基本相反。
点积的顺序无关性
无论是向量v点积向量w,或是相反,它们的点积相同。
向量对称的情况

向量不对称的情况
假设一个向量的长度是另外一个的两倍,此时出现不对称的情况。

将向量v放大两倍并不改变向量w的投影长度
点积公式计算和几何计算上的联系
我们将一个平面变换后成为一个轴,此时它的基向量i和j落在一条直线上
变换前

变换后
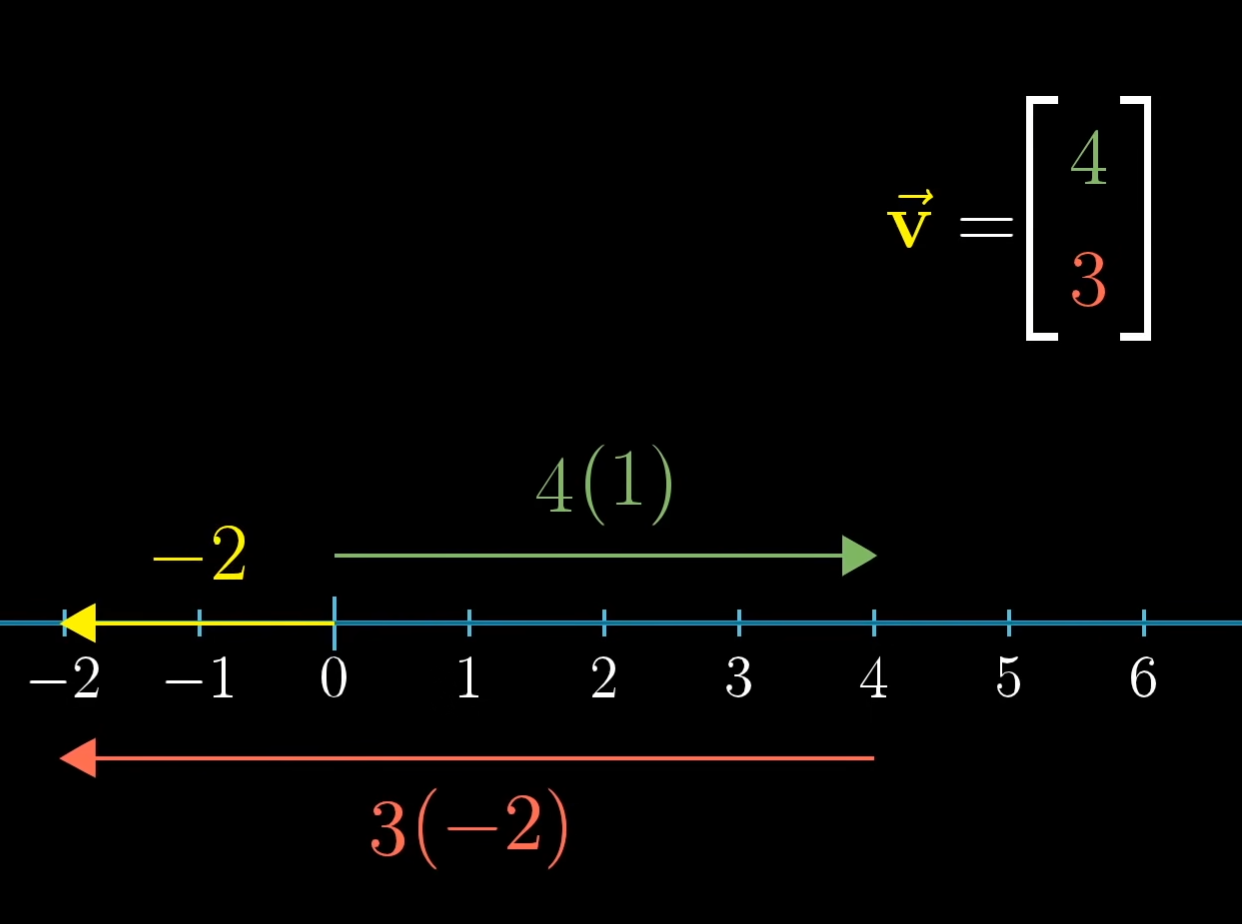
向量v变换后落在-2,所以将3(-2)后移至-2
完全从数值角度计算时,这就是矩阵向量的相乘,而这个1x2的矩阵和向量相乘的运算过程就像两个向量的点积一样。

从下面这张图可以看的更加清楚
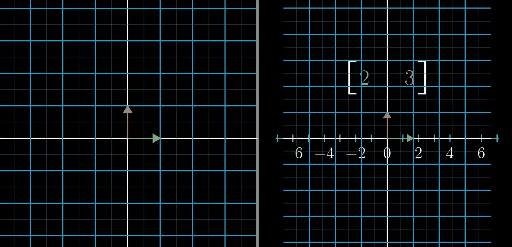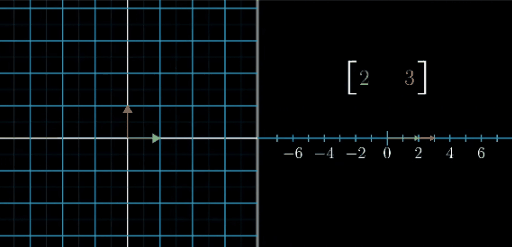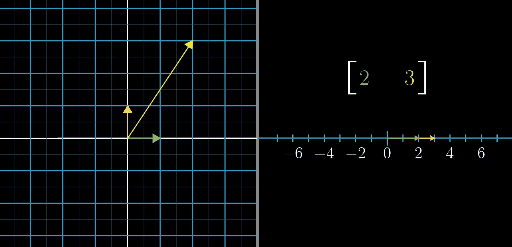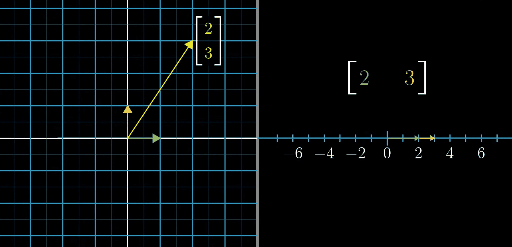
单位向量的情况求证
假设,我们在二维空间中有一条数轴,并且还有一些二维向量,将二维向量直接投影在数轴上。
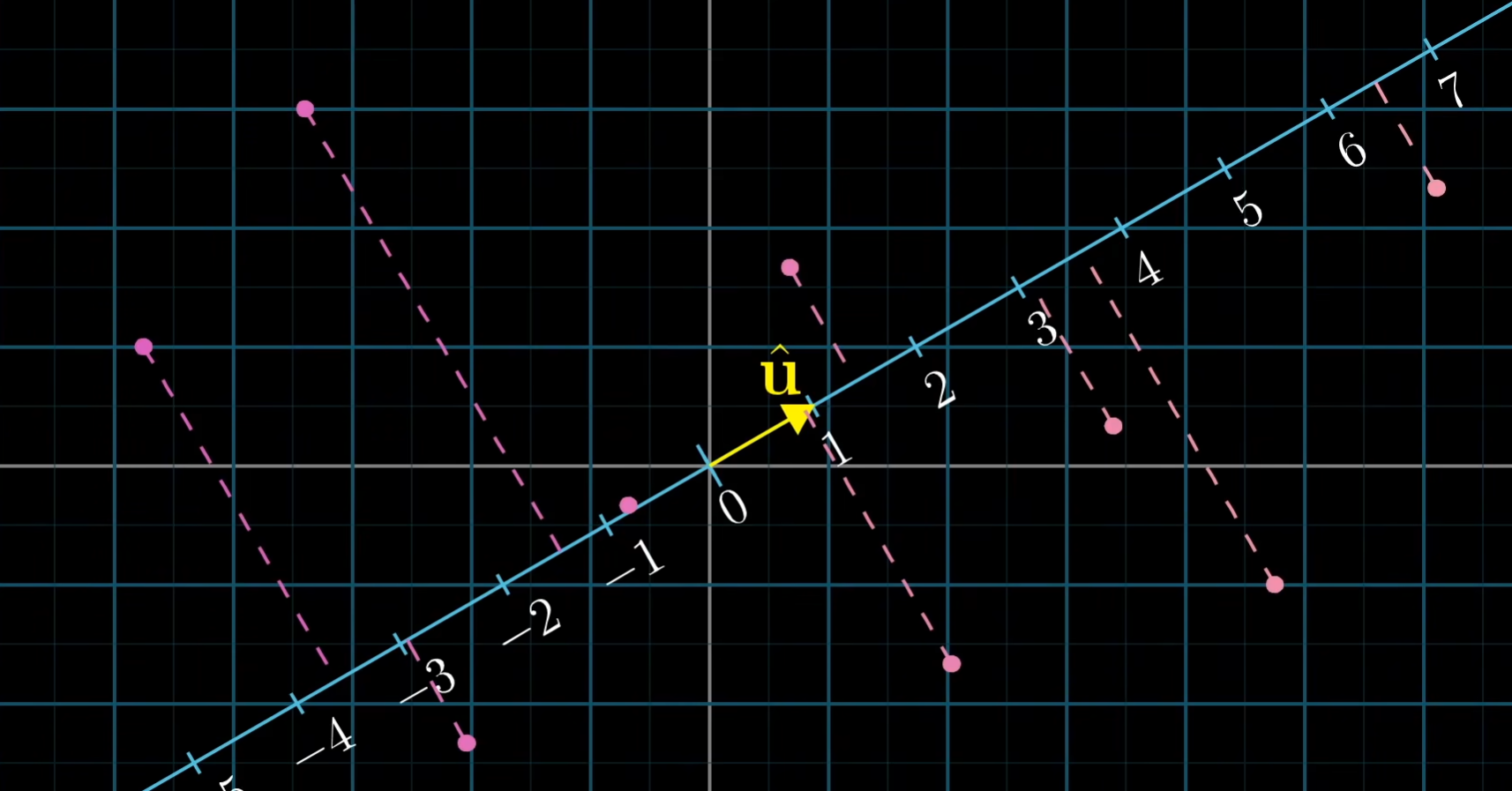
这样我们便定义了一个二维向量到数的函数,该函数是线性的,因为二维空间上等距分布的点投影在数轴上仍然等距。
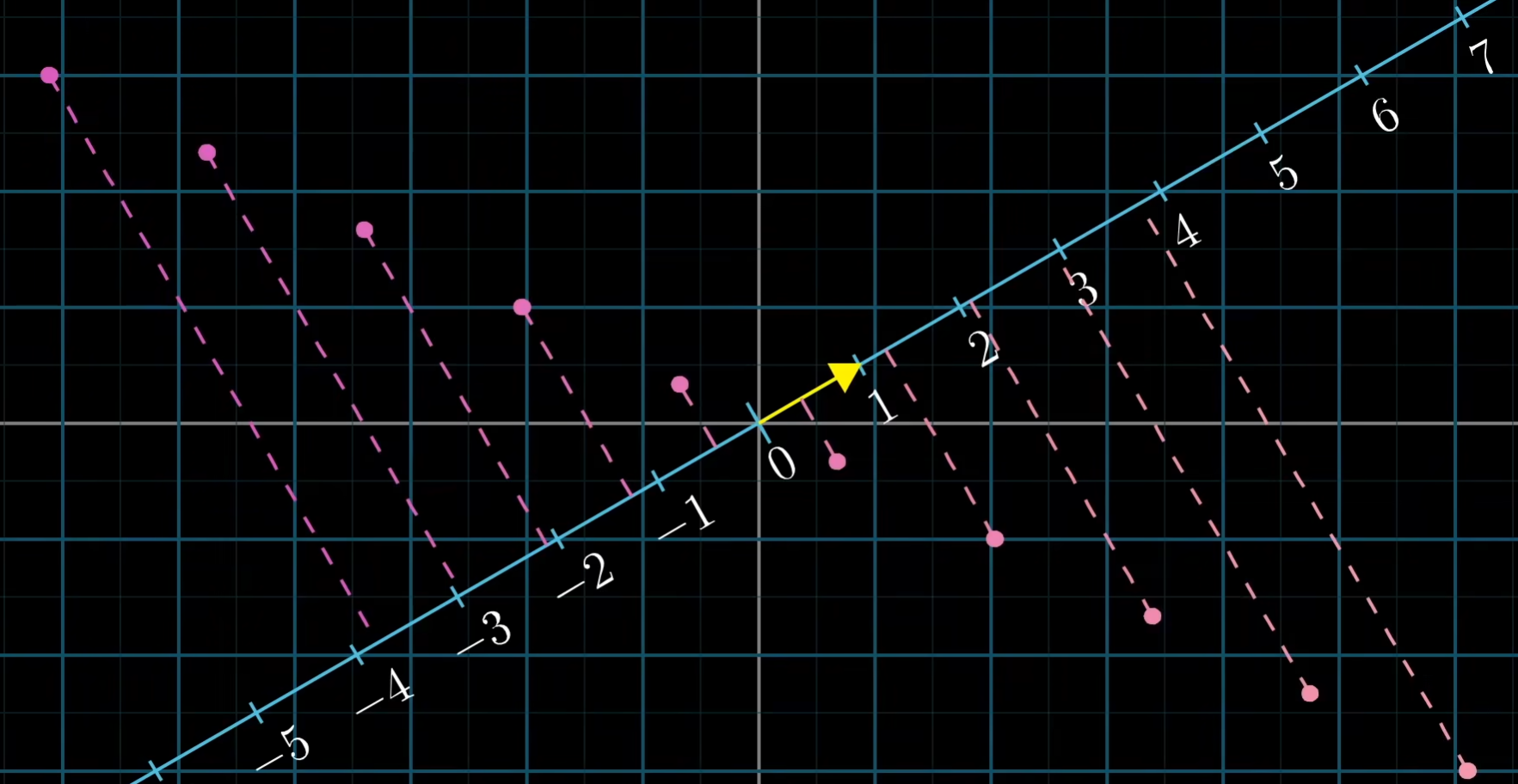
虽然该函数是在一个二维空间中,但是它的输出结果还是一个数,而不是一个二维向量。
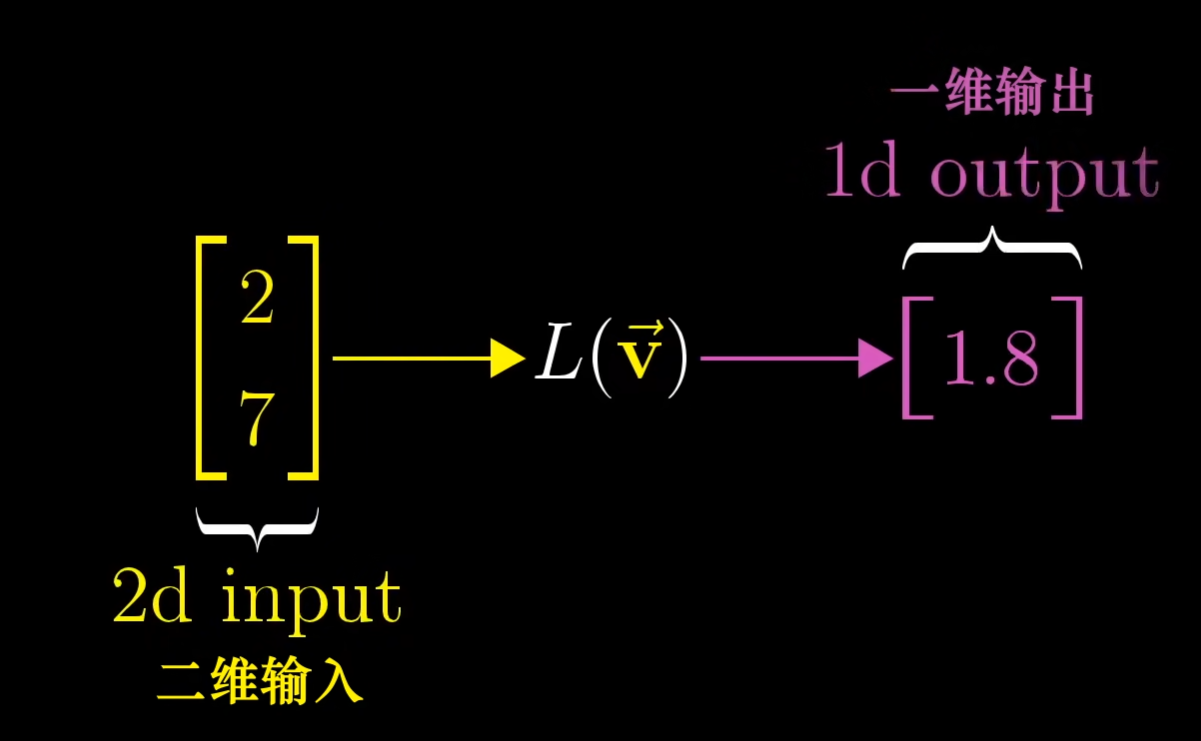
但我们在二维空间中拥有一个向量u,它又碰巧落在数轴上。根据上面的变换,我们可以得到输入一个二维向量,输出一个数,这样我们就能够找到一个1x2的矩阵。为了找到这个矩阵,我们需要考虑到变换后i-hat和j-hat的位置,因为它们是矩阵的列。
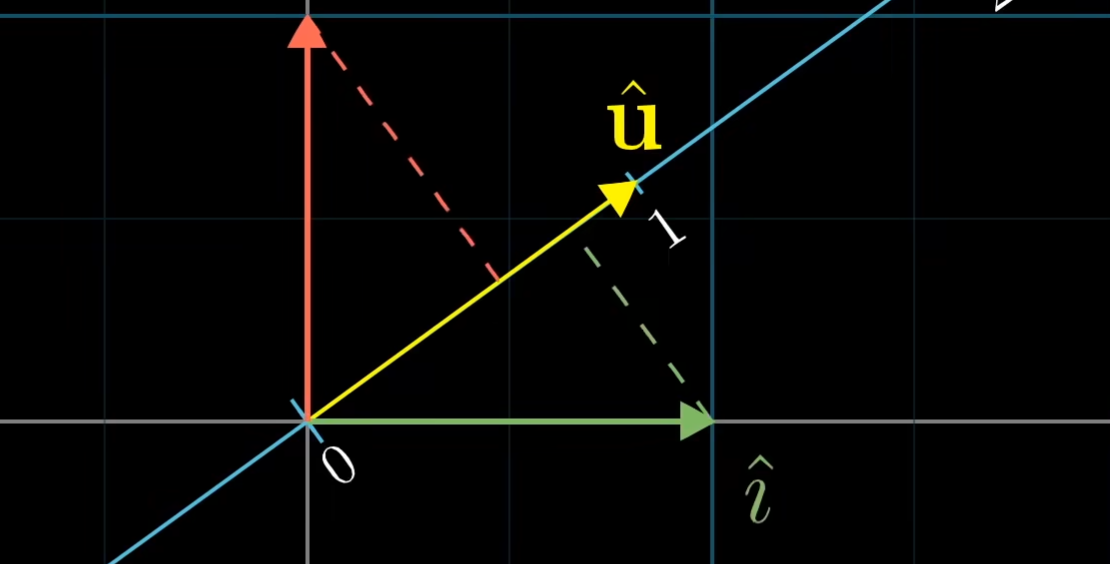
因为i-hat和j-hat都是单位向量,所以i-hat和向量u的投影完全对称。所以向量u在i-hat的投影就是i-hat变换后的位置。

那么,同理可得j-hat变换后的位置。

这样我们就得到了该矩阵,所以描述投影变换的1x2矩阵的两列,就是向量u的两个坐标。
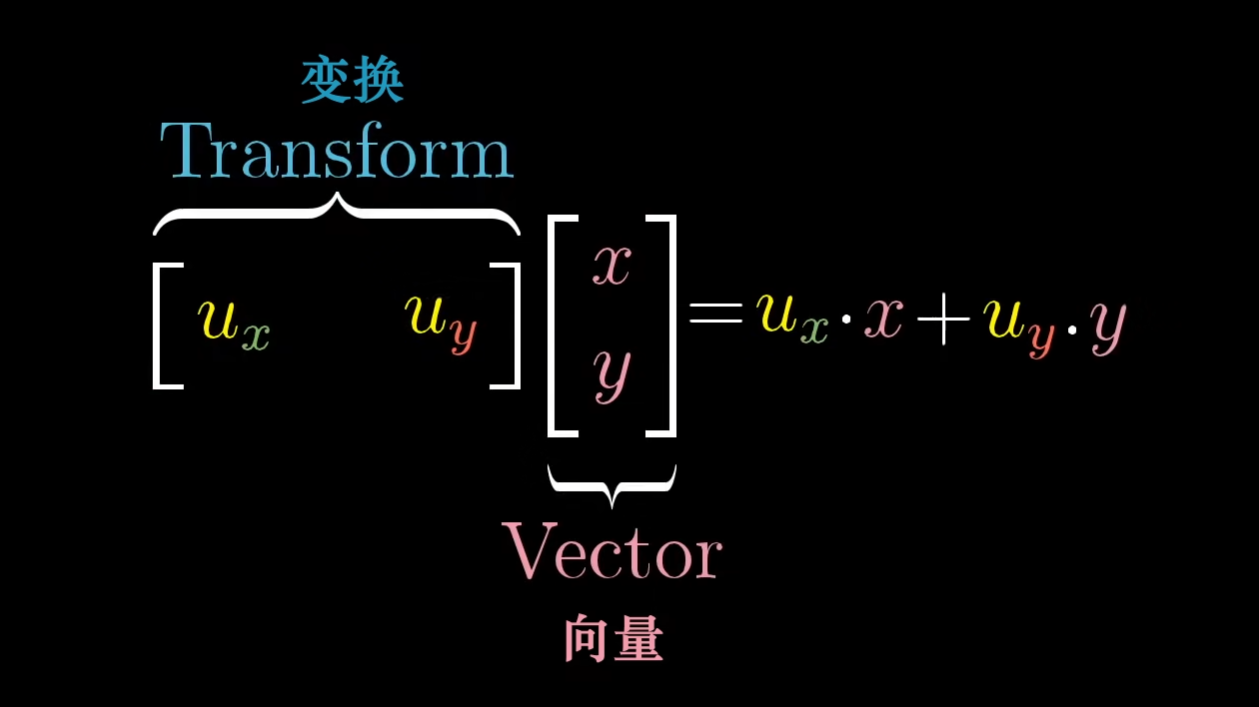
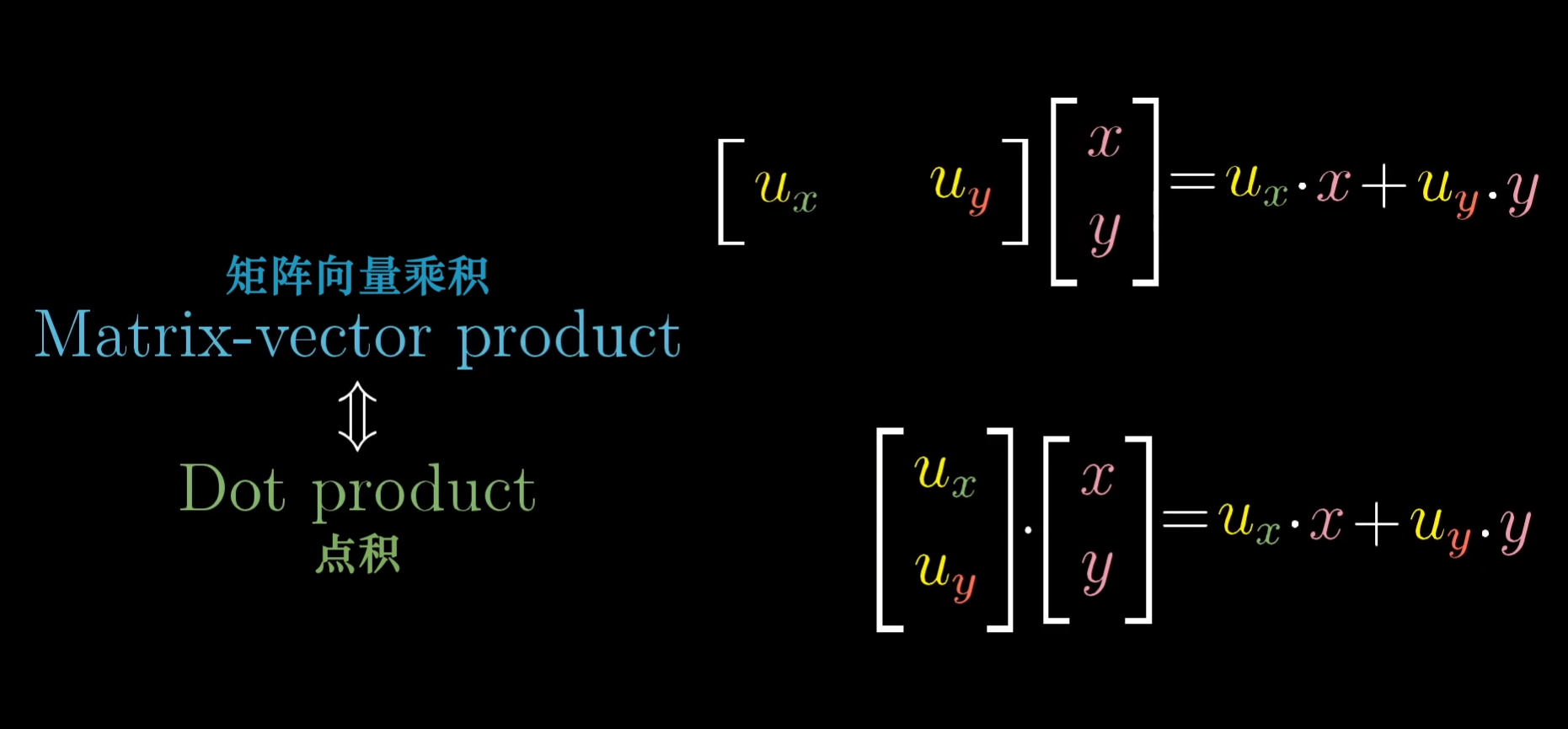
在计算上,与点积的计算完全相同。
所以这就是为什么与单位向量的点积可以理解为向量投影到单位向量所在直线上所得到的投影长度。
非单位向量的情况求证
比如将向量u乘3倍,那么因为该函数是线性的,那么相应的输出也会乘3倍。

投影向量与点积的联系
所以,如果看到任何一个变换的输出空间是一维数轴,无论它是如何定义的,空间中会存在唯一向量v与该变换相关,也就是说该变换和向量v做点积是一样的。
总结
点乘,是理解投影的有利几何工具。在实用领域,可以检查向量的方向关系。最重要的,两个向量的点乘,就是将其中一个向量转化为线性变换。